新浪科技讯 12月22日消息,未来论坛第十一期“理解未来”讲座在北京国际数学研究中心开讲。中国科学院院士、美国普林斯顿大学数学系Higgins讲座教授田刚从几何学角度讲述了数学史上最艰难的课题之一——庞加莱猜想的历史、意义和影响。
在当今社会,我们常常听到各种各样的“数学无用论”,甚至有人调侃:只要会个加减法,够买菜算账就行了。然而讲座甫一开场,田刚教授便向大家传递出一个重要信息:数学是有用的。“整个数学发展的过程对人的思维、对自然和真理的追求都是非常重要的事”。 在古希腊,学习几何被认为是寻求真理的最有效的途径。毫无疑问,数学及数学家对人类文明的进步做出了不可磨灭的贡献,被誉为“最后一位数学全才”的庞加莱也不例外。
一位数学史家曾经如此形容1854年出生的亨利?庞加莱:“有些人仿佛生下来就是为了证明天才的存在,每次看到亨利,我就会听见这个恼人的声音在我耳边响起。”时至今日,庞加莱已经被公认是19世纪末和二十世纪初具有领袖地位的数学家,他在数学方面的杰出探索对20世纪和当今的数学有着极其深远的影响。
庞加莱于1904年提出——任何一个封闭的三维空间,只要它里面所有封闭曲线都可以收缩成一点,这个空间就一定是一个三维圆球。此后,庞加莱猜想就和黎曼假设、霍奇猜想、杨?米尔理论等被并列为七大数学世纪难题。本世纪初,美国克雷数学研究中心宣布为这七大难题悬赏百万美元求解。
庞加莱猜想最终的解决依赖于微分几何和分析的方法,最重要的工具是R.Hamilton提出的里奇曲率流。R. Hamilton证明了里奇曲率流的许多基础性结果,并给出了解决Thurston三维流形几何化猜想的纲领。他也解决了庞加莱猜想的一些特别情形,但他无法克服一些关键技术问题。有趣的是,普林斯顿大学与庞加莱猜想有很深的渊源。无论是尝试过而未成功的数学家中,还是对最终解决做出突出贡献的数学家中,许多都在普林斯顿大学工作或学习过,如J. Whitehead,Papakyriakopoulos,R.Hamilton等等。
直到2002年,俄罗斯数学家佩雷尔曼解决了这个重大猜想。佩雷尔曼的证明,用到了过去50年甚至更长时间微分几何中的许多重要进展,但最终解是他完成的,他的解中间牵涉到很多数学家的工作,包括非负曲率空间的分类,黎曼几何的紧性理论,热传导方程的Harnack型估计,曲率下方有界空间的塌缩理论,极小曲面理论等等。当年《科学》杂志以“本年度科学最大突破”之名承认了他的成就,随后,菲尔兹”奖也授予给了佩雷尔曼,然而,他的举动惊动世人———他竟然拒绝领取这个数学界的诺贝尔奖。理由很简单,“这个奖和我没有关系。如果证据是正确的,每个人都能理解它,那么也不需要什么肯定。”
佩雷尔曼的惊世骇俗令人神往,而欧几里得、高斯、黎曼、庞加莱、这些数学史上的明星也在田刚教授的娓娓道来中熠熠生辉。“数学是非常有用的,只不过有些研究成果暂时还没有得到实际应用”。田刚教授直白质朴的言语让我们再一次认识到了数学作为自然科学基础的重要性。
爱因斯坦曾说:“纯粹数学,就其本质而言,是逻辑思想的诗篇。”数学不仅不枯燥无聊,而且充满美感,然而这美感只有少数幸运儿才能体味。在北京最美的季节,于神圣的学府汇聚一堂,共同聆听这美妙的诗篇,我们有理由相信,我们都是那少数幸运儿中的一员。


 应数而生!伊顿 93Li G2 锂电系统全新登场,全“锂”赋能数据中心发展
应数而生!伊顿 93Li G2 锂电系统全新登场,全“锂”赋能数据中心发展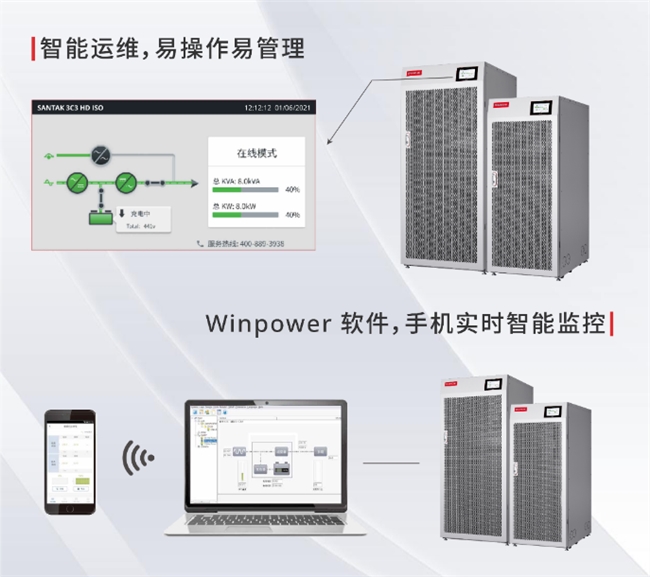 聚力工业,强势焕新!山特 3C3 HD ISO UPS 新品隆重登场
聚力工业,强势焕新!山特 3C3 HD ISO UPS 新品隆重登场 PhotonPay光子易携一体化支付解决方案亮相Money20/20 USA!
PhotonPay光子易携一体化支付解决方案亮相Money20/20 USA! 即刻迁移至 Windows 11,为 Windows 10 支持终止做好准备
即刻迁移至 Windows 11,为 Windows 10 支持终止做好准备 多向联结·为北京市交通出行保驾护航:小鸟科技助力北京市交通应急指挥中
多向联结·为北京市交通出行保驾护航:小鸟科技助力北京市交通应急指挥中 PhotonPay光子易携OTA场景化支付解决方案亮相2024亚洲旅游科技展
PhotonPay光子易携OTA场景化支付解决方案亮相2024亚洲旅游科技展 一场双11内容盛宴 | 抖音电商作者们用好内容迎来双11开门红
一场双11内容盛宴 | 抖音电商作者们用好内容迎来双11开门红 小生意,大爆发|八大行业双11策略划重点
小生意,大爆发|八大行业双11策略划重点